Rolling the Groovy Dice
Jan 6, 2013
Bit of a throw away post but it might save someone 5 minutes… Nothing to do with Project Euler…
I needed to have a quick way of rolling an arbitrary number of polyhedral dice including the ability to take a number of the highest from all those rolled.
I did this in Groovy by adding an overloaded roll() instance method to Integer along with a helper isPolyhedralDie() method (but only to catch me making some sort of basic typo in the calling code).
Integer.metaClass.isPolyhedralDie() {
(delegate as Integer) in [ 3, 4, 6, 8, 10, 12, 20, 100 ]
}
Integer.metaClass.roll() {
delegate.roll(1)
}
Integer.metaClass.roll() { dice, best = dice ->;
assert delegate.isPolyhedralDie() && (best > 0) && (dice >= best)
def ( sides, rnd ) = [ delegate, new Random() ]
(1..dice).collect { rnd.nextInt(sides) + 1 }
.sort().reverse()[0..<best].sum()
}
// Generate 4x 3/4d6 character attribute sets
4.times {
def r = (1..6).collect { 6.roll(4,3) }
r.countBy { it }.sort { a, b -> b.key <=> a.key }
.each { k, v -> print "${v}x $k, " }
println "Sum = ${r.sum()}"
}
Usage:
Integer#roll() // 6.roll() = roll 1d6 Integer#roll(noOfDice) // 6.roll(3) = roll 3d6 Integer#roll(noOfDice, noOfBest) // 6.roll(4,3) = roll 4d6 take 3
Groovin’ in Java
Mar 7, 2012
I’ve just been watching an interesting presentation on using Groovy as an additional toolkit in Java. Groovy excels in handling XML, File I/O and JDBC, as well as offering good support for Collections and Closures (as regular readers of this blog already know!). The type of things you typically need to do day-in-day-out for your regular job.
If you want to learn more about what you can do with Groovy in the real world take a look at the presentation on InfoQ – Improve Your Java with Groovy
The presenter, Ken Kousen, also has a good blog with some very useful information on using Groovy for doing regular & proper programming tasks – the sort of thing it’s really intended for – not what I do here!
He’s got a book in the works, Making Java Groovy, which should be coming out in late 2012.
Project Euler Problem #65
Jan 29, 2012
Read the details of the problem here
Summary
Find the sum of digits in the numerator of the 100th convergent of the continued fraction for e.
Solution
This question immediately reminded me of Problem #57 which ended up being quite a simple solution though it sounded involved initially. I took a look at that, and adopted a similar approach to this one.
The trick with this problem was to spot the pattern as to how the numerator changed down the sequence. As it turned out, the values of the denominator are superflous to this and can just be ignored for this purpose.
Taking the first ten terms as given (with a zeroth term for completeness) given this is how it works:
| Term | Numerator | Multiplier | Formula |
|---|---|---|---|
| 0 | 1 | ||
| 1 | 2 | 2 | 2 * num0 |
| 2 | 3 | 1 | 1 * num1 + num0 |
| 3 | 8 | 2 | 2 * num2 + num1 |
| 4 | 11 | 1 | 1 * num3 + num2 |
| 5 | 19 | 1 | 1 * num4 + num3 |
| 6 | 87 | 4 | 4 * num5 + num4 |
| 7 | 106 | 1 | 1 * num6 + num5 |
| 8 | 193 | 1 | 1 * num7 + num6 |
| 9 | 1264 | 6 | 6 * num8 + num7 |
| 10 | 1457 | 1 | 1 * num9 + num8 |
So this can be summarised as:
numn = muln * numn-1 + numn-2
Where n is the term being calculated and muln is the nth element of the continued fraction. This is simply n / 3 * 2 when n mod 3 == 0, and 1 otherwise.
Given that the multipliers work in triplets, this can be used to advantage and reduce the number of calculations required. I created a function that given the n-1 and n-2 numerators, and a term number could calculate the next three numerators in the sequence. It meant that I didn’t have to do any modulus calculations as long as I kept the boundary aligned correctly i.e. only call it for terms, 2, 5, 8, etc. which were the start of the triplets.
Starting at term 2, I then called this recursively until it was being asked to calculate the 101st term. At this point the 100th term would be the n-1 numerator value and could be returned.
def f(p1, p2, tc) {
if (tc == 101) return p1
def m = p1 + p2
def n = ((tc + 1).intdiv(3) * 2) * m + p1
f(n + m, n, tc + 3)
}
def answer =
(f(2G, 1G, 2).toString() as List)*.toInteger().sum()
This runs in around 115 ms, with sum of the digits taking about 10 ms. A port of this code to Java runs in around 1.3 ms in total.
Conclusion
Groovy was a nice language to do this in. Not having to mess about with BigInteger objects explicitly is always a boon in the Java world. Performance was quite disappointing though – given that f() is only ever called with BigInteger arguments the compiler should be able to work out exactly what types the variables are and the generated bytecode should be pretty similar to that which javac outputs…but it’s not. In this case Groovy is nearly two orders of magnitude slower and I really don’t see a good reason for it at this stage in the language maturity.
Project Euler Problem #243
Jan 21, 2012
Read the details of the problem here
Summary
Find the smallest denominator d, having a resilience R(d) < 15499 ⁄ 94744
Solution
Due to real-life intrusion I haven’t been doing much Project Euler for the last few months but a conversation with a colleague at work the other day brought the subject up and I thought I’d revisit the site.
They’ve changed their format quite a lot now and though it’s still fundamentally the same, the concept of “badges” has been introduced – “awards” above and beyond just the old numbers of puzzles solved (which is now more granular). I’m a sucker for things like that and one of them – “Trinary Triumph” – just needed one more question to complete so it was, as the saying goes, like a red rag to a bull!
The problem was actually worded quite straightforwardly, and a little thought showed that this was very similar to Problem #69 and Problem #70. The numerator in the resilience function is going to be the count of terms that are relatively prime to the denominator i.e. Euler’s Totient (φ) function. The solution to Problem #69 was found by maximising n/φ(n) whereas, in this problem we’re looking to minimize φ(d)/(d-1) – so it’s essentially the same thing. The answer is likely to be found by looking for a number consisting of the product of many small prime factors perhaps with some multiplier (also a product of small primes) i.e. some of those factors may be of a higher power.
Problem #108 and Problem #110 also tackled the domain of products of powers of primes and the solution to the latter seemed a good place to start as the one to the former ended up as being a bit of a lucky hack. As per that solution, taking the approach of assuming that the answer was to be found somewhere at n * product(prime factors) and driving off that meant that factorisation of large numbers wasn’t needed so Groovy would remain a viable language to do this in.
Again, when doing these problems with Groovy, it’s best to try to work out the potential scope ahead of runtime as it doesn’t perform that well at number crunching.
What I did need to how to calculate the totient value for numbers with large numbers of factors – I’d kind of worked it out from a bit of guess work for two factors when doing Problem #70 but this wouldn’t work for this. Luckily Wikipedia came to the rescue giving the formula quite succinctly as:
φ(n) = n(1-1/p1)(1-1/p2)…(1-1/pr).
Using this I found that the product of a prime sequence 2..23 gave a totient above what was being sought, whilst 2..29 was a potential solution itself. The answer probably fell somewhere between these two and this therefore formed the search space.
I then just reused the helper function I’d used in Problem #110 with a bit of an educated guess as to what the maximum power might be. If the multipler was 25 i.e. 32, this would exceed the solution of the longer prime sequence – so a maximum power of 4 seemed reasonable to use. I also seeded the generator function with the assumption that all of the primes between 2..23 were going to be factors – this seemed a reasonable assumption given what I knew of the totient function characteristics.
def gen_powers(range, maxlen, yield) {
gen_powers(range, maxlen, [], yield)
}
def gen_powers(range, maxlen, pows, yield) {
if (pows.size() == maxlen)
yield(pows)
else if (pows.size() == 0)
range.each { gen_powers(range, maxlen, [it], yield) }
else
range.findAll { it >= pows[0] }
.each { gen_powers(range, maxlen, [it]+pows, yield) }
}
def ( answer, TARGET, POWER_RANGE ) = [ Long.MAX_VALUE, 15499/94744, (0..4) ]
def primes = [ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 ]
gen_powers(POWER_RANGE, primes.size(), [1] * primes.size()- 1) { powers ->
def (d, factors) = [ 1G, [] ]
powers.eachWithIndex { v, i ->
d *= primes[i] ** v
if (v > 0) factors << primes[i]
}
if ((d > 1) &&
(answer > d) &&
(((int)(factors.inject(d) { p, v -> p * (1 - 1/v) })) / (d-1) < TARGET)) {
answer = d
}
}
Despite the heavy use of the slow Groovy listops (and a bit of hacky code) this runs in around 940 ms.
Next will be Problem #65, a question on continued fractions, that will give me my “As Easy As Pi” award!
Conclusion
With the upfront analysis on the problem and the re-use of the power generator, Groovy made it easy to put together a terse solution that ran in a reasonable time. When doing the calculation of the value of the denominator I did find myself missing Python’s map() capability to process two lists against a closure and return a result. Sounds like the sort of thing that should be in there, maybe it’s buried in the Groovy docs somewhere…
1. IDEA, 2. Kotlin, 3. Profit.
Jul 29, 2011
I was interested to see that JetBrains, creators of the splendid IntelliJ IDEA IDE amongst other things, are working on their own “better-Java-than-Java” language, Kotlin.
Ostensibly this is to resolve some of the “issues” that the Java language has, whilst being simpler than the currently strongest competitor, Scala. Kotlin is going to be supported as a first-class citizen in the IDEA IDE from around the end of 2011.
There’s a lot of talk on various fora about the need (or lack of) for introducing a new language when others like Scala, Groovy and Clojure are becoming more established. This is similar to the fuss back in April 2011 when Gavin King “leaked” the news that Red Hat were working on their “Ceylon” JVM-hosted language. The public launch of Ceylon is likely to be in the same sort of timescale.
Most of the chatter seems to be about the benefits around the features of the languages, semantic overhead of learning, efficiency of execution, dilution of Java skillsets, etc. All are interesting and sound discussions.
What I’m not seeing is anyone saying about the pure commercial value of a company such as JetBrains or RedHat launching their languages focusing on their their own ecosystems. I don’t believe these guys aren’t doing it for the love of the Java community. They’re doing it for cold, hard cash… any why not?
It’s interesting that JetBrains are saying that Kotlin is intended for “industrial use”. By this I’m expecting the real value-add features (which must be compelling) to be supported in their paid-for “Ultimate” edition of IDEA rather than the free “Community” version and they’re targeting the “enterprise” market.
They would need to convince “corporate” development managers of the benefits of the Kotlin, disabuse them of the risks of selecting a single vendor language and get it embedded into their companies order to monetise the investment in developing it.
That’s not to say they’re wrong to try – look at how successful VB6 was and that’s a single company language supported by a strong IDE!
They’ll have to be quick though.
Java 7 has just been released and Java 8 is due in late 2012. Whilst J7 addresses quite a few “niggles” with Java (including reducing some noise around Generics and the equivalent of C#‘s “using” statement) and add some good features into the JVM it’s not the complete “Project Coin” package.
The “big thing” being sold in all these new languages are Lambdas/Closures which won’t come until J8. (You can see the split of features here.) This means that they’ll have 12 months to get some traction before the “official” Java language supports this.
Personally, I don’t believe that having closures in an OO imperative language is that important. Useful, of course, but not the end of world if they’re lacking. There didn’t seem to be much demand for them in Java before Ruby on Rails became popular in 2006 and there was an outbreak of scripting-envy across the Java community.
Of course, with the JVM bytecode instruction InvokeDynamic being added in Java 7 it means that dynamic language such as JRuby should become much more performant so, if you really want closures on the JVM why not just use that?
I think it’s disappointing that the official Java/JVM ecosystem has been on a bit of a hiatus for the last 5 years (Java 6 was released in 2006) but it’s kind of understandable given the situation with Sun and Oracle. It’s also disappointing that Coin was split across two releases as this will delay adoption too and, in the Java world, allow third-parties to fill the perceived gap with semi-official solutions in the interim.
It will be interesting to see how this all plays out. I do hope it doesn’t distract JetBrain or RedHat/JBoss from continuting to provide world-class platform support for the official Java stack on their products.
Project Euler Problem #86
May 24, 2011
Read the details of the problem here
Summary
Exploring the shortest path from one corner of a cuboid to another.
Solution
It’s been a while since I’ve posted a Project Euler solution and the ones I have posted have been catch-ups. The other day I saw a specific search on this site for a solution to Problem 86 which I hadn’t yet completed so I thought I’d give it a go…
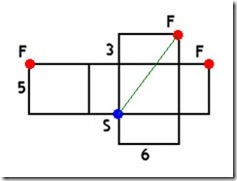
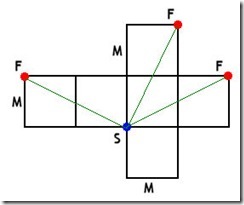
On first reading this seemed a little unclear but it comes apart quite easily with a little prodding and poking. Taking the example that Euler gives and flattening it makes it apparent what’s going on. The shortest path (SF) is the hypotenuse of a Pythagorean triangle with sides of { 6, 8 (3+5), 10 }.
The diagram below shows the case of an M x M x M cuboid to demonstrate the three variants of the shortest path in a very obvious manner.
So it’s just a case of checking for Pythagorean triangles with an adjacent side of length M, and up to 2M for the opposite side. Note that, due to this abstraction from the actual cuboid, it’s not necessary to deal with the other two sides individually – the opposite side length is taken as the total of the depth and height of the cuboid. Once a suitable triangle is found the number of solutions for it, taking into account the ways in which the opposite side length may be composed for any given potential cuboids, are added onto the running total.
def ( answer, solutions ) = [ 1, 0 ]
while (true) {
for (i in 2..(2 * answer)) {
def hyp = Math.sqrt(answer * answer + i * i)
if (hyp == Math.floor(hyp)) {
solutions += (i > answer + 1) ?
(answer + answer + 2 - i).intdiv(2) : i.intdiv(2)
}
}
if (solutions > 1e6) break
answer++
}
The solution is quite succinct and, even though it’s simply a brute force algorithm, runs in around 1.31 seconds – so well within the 15 second target. Smarter algorithms might include changing this one to a bisection search of across the solution space, or maybe pre-generating Pythagorean triangles and driving directly off of those.
Conclusion
Groovy was perfectly fast enough for solving this problem, both in terms of coding and runtime. From a performance perspective it’s advisable to use the Math.floor() function rather than a straight cast to (int) and calling intdiv() is also a must compared to a straight division.
Project Euler Problem #92
Sep 11, 2010
Read the details of the problem here
Summary
Investigating a square digits number chain with a surprising property.
Solution
Simple and straight-forward non-mathematical problem to solve. I coded up the following program – note that after one pass the value of the sum of the squares will reduce to 7×92 (or 567) at most so the cache is relatively small for the entire range of numbers.
def LIMIT = 10000000
def CACHE_SIZE = 9 * 9 * 7
def sumsOfSquares = new int[CACHE_SIZE+1]
Arrays.fill(sumsOfSquares,0)
sumsOfSquares[1] = 1
sumsOfSquares[89] = 89
def answer = 0
for (i in 2..LIMIT) {
def sum = i
while ((sum != 1) && (sum != 89)) {
def n = sum
sum = 0
for (c in n.toString()) {
def v = c.toInteger()
sum += v * v
}
if (sumsOfSquares[sum] != 0) sum = sumsOfSquares[sum]
}
if (i <= CACHE_SIZE) sumsOfSquares[i] = sum
if (sum == 89) answer++
}
This ran in 36.14 seconds so it was well outside my 15 second target. I did some tweaks to the code converting it into to a recursive function and trying some extra cache lookups at the beginning of the calculation but only managed to reduce the runtime down to 31.81 seconds. (Using Groovy listops rather than the explicit loops for calculating the sum pushes the time out to over 2 minutes.) Although a straight Java conversion would probably run in a second or two I felt that some improvement could be made to the algorithm as the curent solution didn’t really use much of one to speak of.
The obvious observation is that the sum of squares function is being performed many times for numbers that are fundamentally the same as the sum will be the same for all permutations of a given set of digits i.e. the number 3241218, is the same as 2314821 or 1122348. A quick experiment revealed that there are only 11,440 such unique permutations – that would reduce the number of times the expensive summing operation had to be called by a factor of around 870.
In order to maintain the count it would be necessary to know many times a given set of digits can occur in the full 107 range. This is simply the factorial of the total number of elements divided by the product of the factorials of the counts of the unique elements.
As there were only a total of 7 digits I could have just coded nested loops to construct the numbers but I already had a generator for such a purpose built as part of the solution to Problem #110. This generates the digits in descending order and is general purpose but would do the job easily though, as it uses Groovy listops, isn’t the fastest means.
So it was just a case of pre-populating the cache, generating the unique digit sequences, calculating the initial sum of squares, pulling the terminal result from the cache and, for those that resulted in 89 getting the multiples of that to add to the total.
def sumOfSquares(n) {
def sum = 0
for (c in n.toString()) {
def v = c.toInteger()
sum += v * v
}
return sum
}
def permutations(n) {
def factorials = [ 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880 ]
def s = 1
for (i in n) {
s *= factorials[i]
}
return factorials[7].intdiv(s)
}
def gen_digits(range, maxlen, yield) {
gen_digits(range, maxlen, [], yield)
}
def gen_digits(range, maxlen, digits, yield) {
if (digits.size() == maxlen)
yield(digits)
else if (digits.size() == 0)
range.each { gen_digits(range, maxlen, [it], yield) }
else
range.findAll { it >= digits[0] }
.each { gen_digits(range, maxlen, [it]+digits, yield) }
}
def MAX = 9 * 9 * 7
def sumsOfSquares = new int[MAX+1]
Arrays.fill(sumsOfSquares,0)
sumsOfSquares[1] = 1
sumsOfSquares[89] = 89
for (i in 2..MAX) {
def sum = i
while ((sum != 1) && (sum != 89)) {
sum = sumOfSquares(sum)
if (sumsOfSquares[sum] != 0) sum = sumsOfSquares[sum]
}
sumsOfSquares[i] = sum
}
def answer = 0
gen_digits((0..9), 7) { digits ->
def sum = sumsOfSquares[sumOfSquares(digits.join().toInteger())]
if (sum == 89) {
def nn = new int[10]
digits.each { nn[it]++ }
answer += permutations(nn)
}
}
It’s all a little too verbose for my liking but does run in 0.57 seconds so nicely succeeds in the objective. Expanding out the listops to explicit loops in the gen_digits() generator method reduces the runtime to 0.36 seconds – a substantial saving of 37% but at the expense of a few more lines of code.
Conclusion
Groovy general “slowness” meant that some “cleverness” was required to get this to execute in a reasonable amount of time. If I’d been using C++ or native Java for this I would have just stuck with the simple initial approach.
Project Euler Problem #112
Sep 5, 2010
Read the details of the problem here
Summary
Investigating the density of “bouncy” numbers.
Solution
The problem reads as being relatively straightforward and fairly non-mathematical in nature (though I can see that it might have to become a statistical problem on a larger scale) so, before I tried anything too clever I went for a simple brute force approach. I just looked to see if the digits of the number were already sorted in either ascending or descending order.
def (answer, b) = [ 100, 0 ]
while (true) {
def s = answer.toString()
def sorted = (s as List).sort().join()
if ((s != sorted) && (s != sorted.reverse())) b++
if (answer * 0.99 == b) break
answer++
}
This runs in 13.24 seconds and so just sneaks in under the wire to satisfies my success conditions!
This did seem a little slow though and replacing lines 4-6 in the solution above with a call to the method below brought the runtime down to 10.59 seconds.
def isBouncy(n) {
def s = n.toString()
def direction = 0
def len = s.length()
for (i in 1..<len) {
if (direction == 1 && (s[i] < s[i-1])) return true
if (direction == -1 && (s[i] > s[i-1])) return true
if (direction == 0) {
if (s[i] > s[i-1]) {
direction = 1
}
else if (s[i] < s[i-1]) {
direction = -1
}
}
}
return false
}
Is the added complexity worth that reduction of 20%? In this case, probably not!
Conclusion
Groovy made this a nice, terse solution. Performance wasn’t excellent but the solution was quick to write and easy to understand when reading it back.
Project Euler Problem #97
Sep 5, 2010
Read the details of the problem here
Summary
Find the last ten digits of the non-Mersenne prime: 28433 × 27830457 + 1.
Solution
Easy to translate straight into code as it stands. No working out necessary!
def PREC = 10G ** 10
def answer =
(2G.modPow(7830457G, PREC) * 28433G + 1G).mod(PREC)
This runs in 18 ms. A Java version, using long-hand BigInteger syntax takes about 1 ms – so around 18x faster. That’s the cost of syntactic sugar in Groovy.
Conclusion
This was one of those “if you’ve got it, flaunt it” problems. The combination of the powerful JVM and convenient Groovy syntax for BigInteger support made for a simple solution albeit less performant than a native Java implementation.
Project Euler Problem #77
Sep 4, 2010
Read the details of the problem here
Summary
What is the first value which can be written as the sum of primes in over five thousand different ways?
Solution
Straightforward and quick to solve using the solutions to Problem #31 and Problem #76 as a starter. The values of primes just replace the values of coins from Problem #31. It’s a quick hack to wrap it in a loop that increments total and selects a suitable list of primes to work with on each iteration.
def primes =
(1..<100).findAll { new BigInteger(it).isProbablePrime(100) }
def ( answer, total ) = [ 0, 11 ]
while (!answer) {
def nways = [1] + [0]*total
primes.findAll { it < total }.each { prime ->
prime.upto(total) { nways[it] += nways[it - prime] }
}
if (nways[total] > 5000) answer = total
total++
}
This runs in 190 ms. It’s not the most efficient of algorithms but it’s well within my 15 seconds target. The length of the prime list was arbitrary but sufficient.
Conclusion
Groovy’s listops made the solution terse to write but nothing that couldn’t be done in normal Java.